Application of Newton's Laws of Motion: Connected Motion, Examples
Application Of Newton Laws Of Motion, Pulley, Connected Motion, Practice Problems, FAQs
Let’s say that you want to roll a ball on a very long frictionless horizontal surface with constant velocity. Is force required to apply on the ball throughout the motion? If you are an Avengers fan you must have seen the Iron Man movie. You must have wondered how Tony Stark is able to fly when he wears the suit? If you are familiar with Newton’s laws of motion then you will be able to answer these questions. Newton’s
Table of Contents
- Pulley
- Connected motion and reaction force
- Practice problems
- FAQs
Application Of Newton Laws Of Motion, Pulley, Connected Motion, Practice Problems, FAQs
Let’s say that you want to roll a ball on a very long frictionless horizontal surface with constant velocity. Is force required to apply on the ball throughout the motion? If you are an Avengers fan you must have seen the Iron Man movie. You must have wondered how Tony Stark is able to fly when he wears the suit? If you are familiar with Newton’s laws of motion then you will be able to answer these questions. Newton’s
Table of Contents
- Pulley
- Connected motion and reaction force
- Practice problems
- FAQs
Pulley
A pulley is a wheel that carries a flexible rope, cord, cable, chain, or belt on its rim. Pulleys are used singly or in combination to transmit energy and motion.
Types of Pulleys
Single fixed pulley: Axis of the pulley is fixed Single movable pulley: Axis of the pulley is not fixed
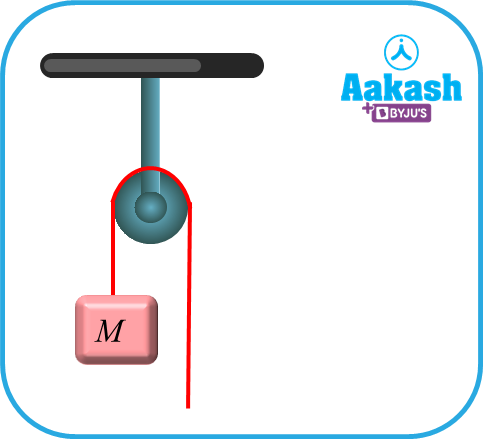

Assumptions to consider for ideal pulley and rope systems
- The rope is massless and inextensible.
- The pulley is light, massless, and frictionless.
FBD of a pulley
- Tension always acts away from the body.
- The same tension will be carried throughout the same rope passing over the pulley.

Pulley Block System
Consider that two blocks of mass m1 and m2 ( )are connected by an ideal string and are kept over a pulley as shown in the figure.Such simple machine is known as Atwood machine. Find the tension in the string and acceleration of blocks?
)are connected by an ideal string and are kept over a pulley as shown in the figure.Such simple machine is known as Atwood machine. Find the tension in the string and acceleration of blocks?

Following procedure is carried out to find the acceleration of masses and the tension in the strings in this kind of a problem.
Step 1:
Assume the direction of accelerations and draw an FBD for all the given masses. If required, resolve the forces along the axes. Assuming ( )
)

Step 2:
Write the equations using Newton’s second law along each axis and for each block.
For block m1,
 ………..……(1)
………..……(1)
For block m2,
 …………….(2)
…………….(2)
As the string is inextensible, both masses move with the same acceleration.
Thus,
 …………………………….(3)
…………………………….(3)
Step 3:
Solve the obtained equations.
Solving the three equations, we get,
Acceleration of masses

Tension in string

A pulley is a wheel that carries a flexible rope, cord, cable, chain, or belt on its rim. Pulleys are used singly or in combination to transmit energy and motion.
Types of Pulleys
| Single fixed pulley: Axis of the pulley is fixed | Single movable pulley: Axis of the pulley is not fixed |
Assumptions to consider for ideal pulley and rope systems
- The rope is massless and inextensible.
- The pulley is light, massless, and frictionless.
FBD of a pulley
- Tension always acts away from the body.
- The same tension will be carried throughout the same rope passing over the pulley.
Pulley Block System
Consider that two blocks of mass m1 and m2 ()are connected by an ideal string and are kept over a pulley as shown in the figure.Such simple machine is known as Atwood machine. Find the tension in the string and acceleration of blocks?
Following procedure is carried out to find the acceleration of masses and the tension in the strings in this kind of a problem.
Step 1:
Assume the direction of accelerations and draw an FBD for all the given masses. If required, resolve the forces along the axes. Assuming ()
Step 2:
Write the equations using Newton’s second law along each axis and for each block.
For block m1,
………..……(1)
For block m2,
…………….(2)
As the string is inextensible, both masses move with the same acceleration.
Thus,
…………………………….(3)
Step 3:
Solve the obtained equations.
Solving the three equations, we get,
Acceleration of masses
Tension in string
Connected Motion and Reaction force
In the given figure, find the expression of acceleration, the tension in the string, and the amount of force exerted by the string on the pulley. (Assume that the table is smooth)

Solution
Here, the weight of mass m1 is acting downward. This weight causes an imbalance and the system moves. The weight of mass m2 will be balanced by a normal reaction, it is moving on a horizontal plane, and it will neither support nor oppose the motion.

FBD for mass m1

Along y-direction,
 ………..(1)
………..(1)
Tension can be found from the force balance of m2 as well
FBD for mass m2

Along x-direction,
 …………….(2)
…………….(2)
Solving two equations we get,


Force exerted by the string on the pulley
FBD of the pulley
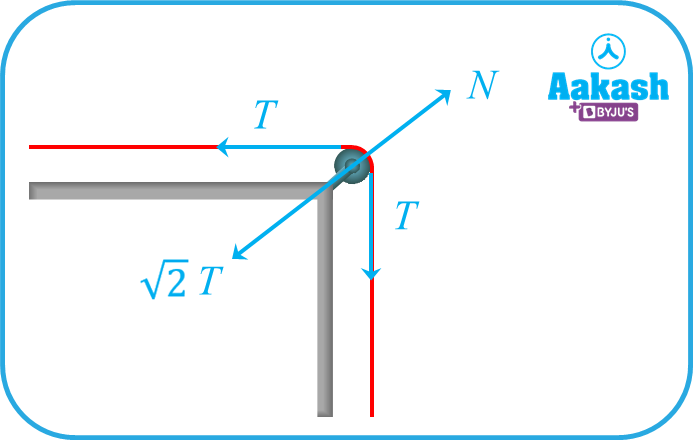
The tension force in string acts tangentially on the pulley. As there are two tension forces at 90o to each other, the resultant force acting will be 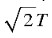
There will also be a normal reaction to the tension force acting in the opposite direction.
In the given figure, find the expression of acceleration, the tension in the string, and the amount of force exerted by the string on the pulley. (Assume that the table is smooth)
Solution
Here, the weight of mass m1 is acting downward. This weight causes an imbalance and the system moves. The weight of mass m2 will be balanced by a normal reaction, it is moving on a horizontal plane, and it will neither support nor oppose the motion.
FBD for mass m1
Along y-direction,
………..(1)
Tension can be found from the force balance of m2 as well
FBD for mass m2
Along x-direction,
…………….(2)
Solving two equations we get,
Force exerted by the string on the pulley
FBD of the pulley
The tension force in string acts tangentially on the pulley. As there are two tension forces at 90o to each other, the resultant force acting will be ![]()
There will also be a normal reaction to the tension force acting in the opposite direction.
Practice problems
Q 1. After the blocks are released from rest, calculate the acceleration of the system and the amount of tension in the string. (Take g = 10 ms-2)

Solution: As the 3 kg block is heavier, it will go down. Hence, take direction of acceleration for the 2 kg block upward and for the 3 kg block downward.
FBD for the 2 kg block

Along y-direction,
 ……..(1)
……..(1)
FBD for the 3 kg block

Along y-direction,
 ……..(2)
……..(2)
Solving equation (i) and equation (ii) simultaneously,
a = 2 ms-2
T = 24 N
Q 2. A force of 100 𝑁 is applied on a 6 kg block that is connected to a 2 kg block with a uniform rope of mass 2 kg. Find the acceleration of the system. (Assume the surface to be smooth)

Considering the rope is inextensible, both masses will move together with the same acceleration due to the 100 N external force.
Consider the masses and the rope together as a system.

Along x-direction,




Q 3. A block of mass m is resting on a smooth wedge of angle 𝜃 as shown in the figure. The wedge is given an acceleration a. What is the minimum value of a so that the mass m doesn’t slide down?

Solution:
Using wedge frame (Non-inertial),
For the observer in the wedge frame, pseudo force needs to be applied on the block in the opposite direction of the motion of the wedge.
FBD of the block,

Along x-direction,



Q 4. The body of mass 10 𝑘𝑔 is placed on a wedge (fixed to the ground) inclined at 60o to the horizontal and released. What is the magnitude of velocity of the block after 1 sec?

Solution: FBD for the 10 kg block is as follows:

Here, the x-axis is chosen along the downward inclined surface as the acceleration of the body will be along this direction.



By using kinematic equations,



Q 1. After the blocks are released from rest, calculate the acceleration of the system and the amount of tension in the string. (Take g = 10 ms-2)
Solution: As the 3 kg block is heavier, it will go down. Hence, take direction of acceleration for the 2 kg block upward and for the 3 kg block downward.
FBD for the 2 kg block
Along y-direction,
……..(1)
FBD for the 3 kg block
Along y-direction,
……..(2)
Solving equation (i) and equation (ii) simultaneously,
a = 2 ms-2
T = 24 N
Q 2. A force of 100 𝑁 is applied on a 6 kg block that is connected to a 2 kg block with a uniform rope of mass 2 kg. Find the acceleration of the system. (Assume the surface to be smooth)
Considering the rope is inextensible, both masses will move together with the same acceleration due to the 100 N external force.
Consider the masses and the rope together as a system.
Along x-direction,
Q 3. A block of mass m is resting on a smooth wedge of angle 𝜃 as shown in the figure. The wedge is given an acceleration a. What is the minimum value of a so that the mass m doesn’t slide down?
Solution:
Using wedge frame (Non-inertial),
For the observer in the wedge frame, pseudo force needs to be applied on the block in the opposite direction of the motion of the wedge.
FBD of the block,
Along x-direction,
Q 4. The body of mass 10 𝑘𝑔 is placed on a wedge (fixed to the ground) inclined at 60o to the horizontal and released. What is the magnitude of velocity of the block after 1 sec?
Solution: FBD for the 10 kg block is as follows:
Here, the x-axis is chosen along the downward inclined surface as the acceleration of the body will be along this direction.
By using kinematic equations,
FAQs
Q 1. Can we use Newton’s second law of motion in a non-inertial frame of reference?
Solution: No, Newton’s laws are not valid in a non-inertial frame of reference. To use Newton's laws in a non-inertial frame you have to apply pseudo force.
Q 2. What is inertia ?
Solution: The resistance of a particle to change its state of rest or of uniform motion along a straight line is called inertia.
Q 3. Give an example of application of Newton’s law of motion?
Solution: Newton’s laws of motion have tremendous applications in our day to day life. One such application is the propulsion of rockets in the sky.
Q 4. Is an external force required to keep a body in uniform motion?
Solution: No
Q 1. Can we use Newton’s second law of motion in a non-inertial frame of reference?
Solution: No, Newton’s laws are not valid in a non-inertial frame of reference. To use Newton's laws in a non-inertial frame you have to apply pseudo force.
Q 2. What is inertia ?
Solution: The resistance of a particle to change its state of rest or of uniform motion along a straight line is called inertia.
Q 3. Give an example of application of Newton’s law of motion?
Solution: Newton’s laws of motion have tremendous applications in our day to day life. One such application is the propulsion of rockets in the sky.
Q 4. Is an external force required to keep a body in uniform motion?
Solution: No